Frozen Thermalization
Liviu Chirondojan and Gian-Luca Oppo have published a Physical Review Letter (122, 084102 (2019)) about an unexpected freezing of thermal relaxation to equilibrium in a European collaboration with Stefano Iubini (Padova, Italy), Paolo Politi (Florence, Italy) and Antonio Politi (Aberdeen, Scotland). The work was supported by the Carnegie Trust for Scotland.
We studied a universal model of lattice interactions, the discrete nonlinear Schroedinger equation, that successfully describes physical systems as diverse as Bose-Einstein condensates in optical lattices and light propagating in an array of optical fibres. When the initial energy is concentrated in just few sites of the lattice, a soliton shape known as ‘discrete breather’ and corresponding to a large central intensity peak, is excited. This single intensity peak is expected to be re-absorbed by the surrounding noisy background via normal thermalization. We instead observed that the discrete breather can survive for astronomical times through a dynamical decoupling with the surrounding. The left panel of Figure 1 shows the dynamics of the breather peak for different initial sizes. High peaks die very slowly. The right panel of the figure shows the diffusion constant that characterises the decay of the breather peak into the surrounding. It decreases exponentially with the initial peak size. In a simple analogy, a high breather is like a floating iceberg that stubbornly refuses to melt and is ready to create havoc.
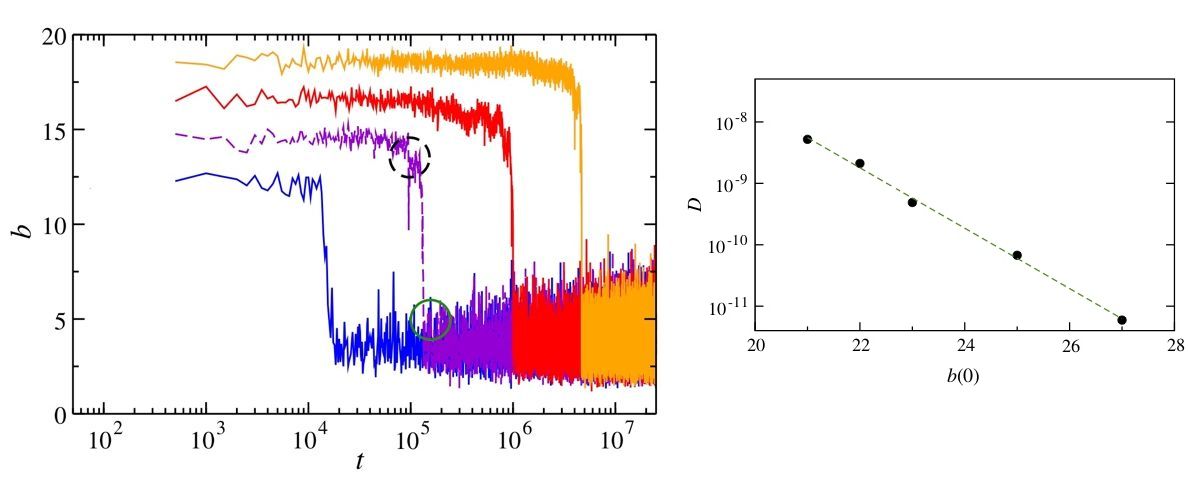
Left panel: the temporal evolution of the breather peak b(t) for different initial sizes (small (blue), intermediate (purple and red), large (orange)). Right panel: the diffusion constant D that characterises the decay of the breather peak into the background versus the initial amplitude of the breather peak b(0).
March 2019