Back in the 1960s mathematicians began to talk seriously about a future governed by nonlinear systems theory, and there was a real excitement about the potential for chaos theory and the rather new world of qualitative dynamics that was unfolding more widely then. We were told that butterflies that flapped their wings in Tokyo could cause a tornado in Tennessee, and by the nineteen eighties a series of specialist and populist books had emerged explaining the science behind these intriguing ideas, and the message that very small changes in one variable could drive enormous changes in another began to sink into the public consciousness. The so-called ‘butterfly effect’ had found an appreciative audience at last.
These things are true and not just in meteorology. Science has shown that the relationships between small changes and large results are endemic to so many things in our world, from weather, to international economics, through to planetary motions, vibrations in structures, motions in fluids, and even territorial behaviour in animals.
We also see the fractal structures that underpin chaos theory also appearing in nature, in the form of infinitely complex patterns across the so-called five patterns of spiral, meander, explosion, packing, and branching. Fractal structures can also be found in computers system architectures, information and data management, human psychology, time, sound, art, and even in law. These arrangements are self-similar across different scales, they are infinitely complex, and every part of a fractal, no matter how much you zoom in or out, looks very similar to the whole image. We now have formal mathematics to support chaos theory together with a powerful and classical stability theory, and this is supported by a highly evolved language for bifurcation, which occur when a small smooth change made to the parameter values – known as the bifurcation parameters - of a system causes a sudden qualitative or topological change in its behaviour. From all this a large and sophisticated toolbox of numerical computational methods has systematically emerged since the seventies, to give graphical form and structure to these relatively new ideas, leading to the science that we now call nonlinear dynamics.
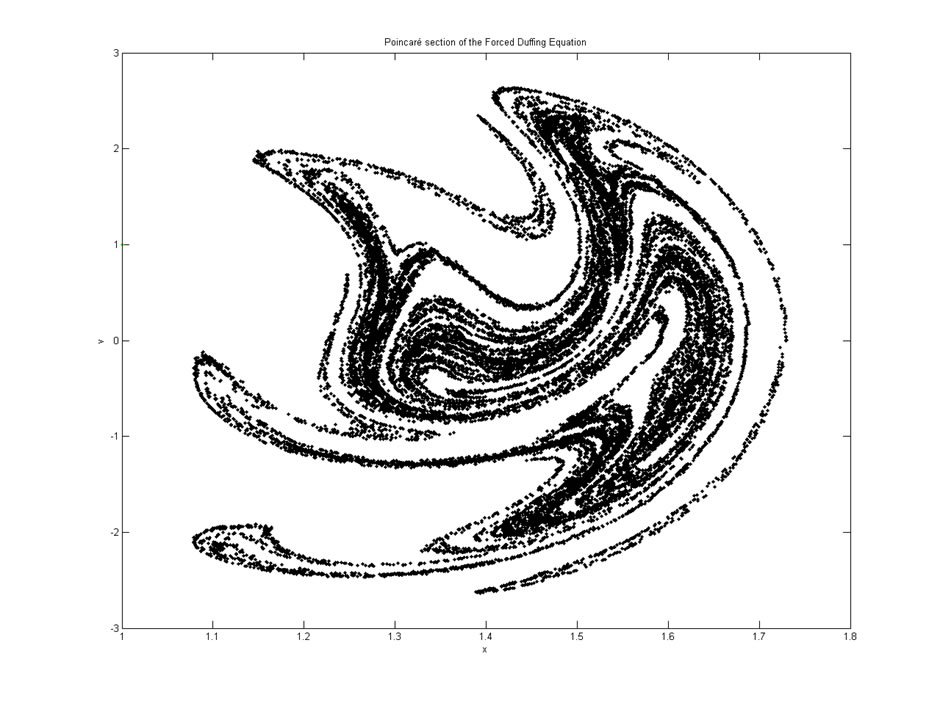
Figure 1 : Duffing Chaotic attractor,
By JJ Harrison (https://www.jjharrison.com.au/ ) - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=16998146
University research has always been central to the development of this subject, mostly because it’s deeply rooted in formal mathematics in parallel with powerful computation and ever evolving computer hardware. The universities, together with the computer industry, have provided exactly the right environment for developing these theories, technologies, and systems to the point where many of the tools of nonlinear dynamics have become embedded within the software packages that students, scientists, and engineers routinely use.
The last few decades have certainly shown that nonlinear dynamics can be used to explain a great deal of what we see in science and what we can synthesise in engineering, but it’s status as a useful subject in its own right, rather than an esoteric curiosity, has traditionally been less clear. More recent thinking, over the last twenty years or so, has shown that nonlinear dynamics is actually endemic to everything we try to do in science, in one way or another, and that we need to start to see it as a fundamental basis for thought and a necessary enabler for design. The world in which we live is not linear, never has been, and never will be. Nonlinearity is the bed-rock of virtually everything and linear models are just simplifications we use when we need quick straightforward answers for a restricted problem.
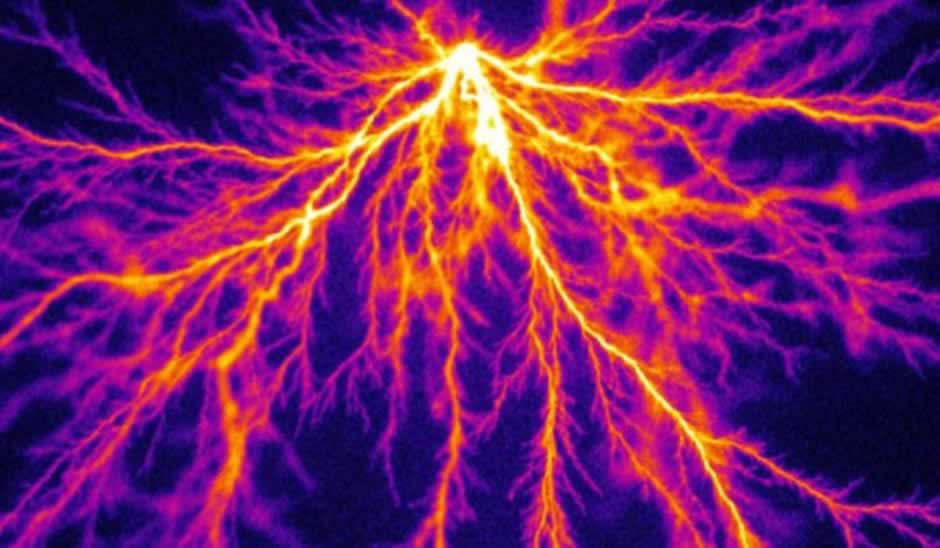
Figure 2 : Electrical discharge streamers containing nonlinear fractal structures within
The figure was published originally in Figure 7 of S. Nijdam et al., 2010 J. Phys. D: Appl. Phys. 43 145204.
In my research all I do has to be expressible in terms of differential equations of one sort or another, and this has led me to nonlinear ordinary or partial differential equation models, many of which have been hard or impossible to solve using standard textbook techniques. In fact, equation solving forms a big part of my own take on the subject. While numerical methods are brilliant for looking into the corners of new phenomena, and can lead us to the deepest insights and the most robust designs, they’re not absolutely the full story so the quest goes on for stable and robust solutions to the nonlinear equations that naturally arise when considering systems as inherently nonlinear.
Over the years I’ve been interested in mechanical vibrations and oscillations – a super-rich area for nonlinear phenomena – and this naturally led me into thinking more about asymptotic mathematical methods and perturbation theories, which in turn eventually allowed me, by the mid nineteen-nineties, to hitch an imaginary lift into space so we could really start to think about the dynamics of large structures on orbit. This resulted in new ideas for space tethers and webs, with all their potential for propulsion and structural synthesis and design in space.
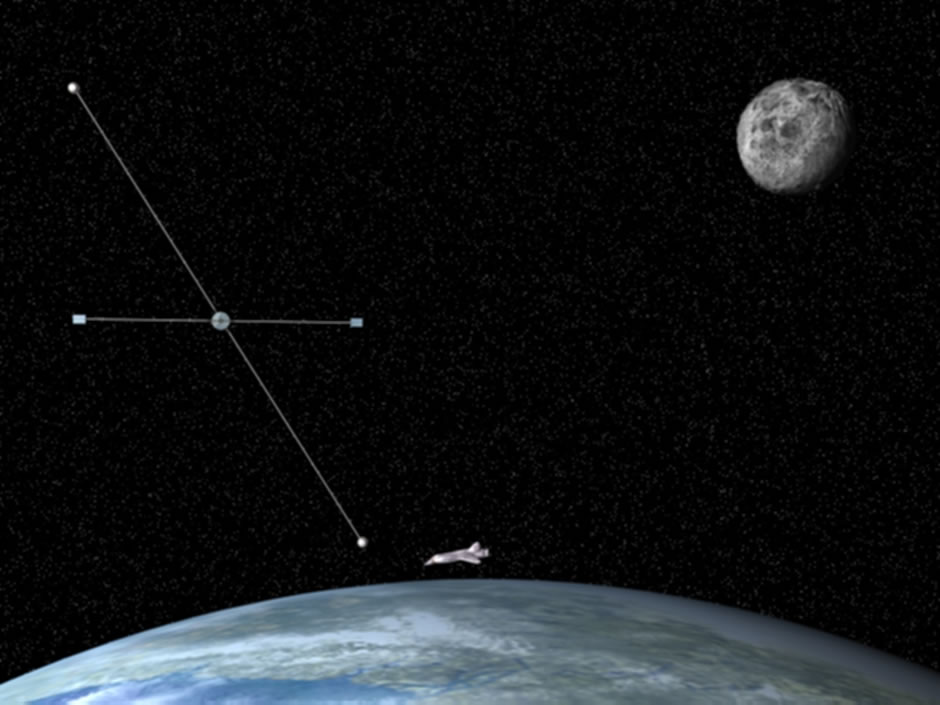
Figure 3 : Concept of motorised tether in Low Earth Orbit
Copyright – Matthew P. Cartmell
Symbolic computing came on the scene as a commercial tool in the nineteen-eighties and ever since then has offered a remarkable opportunity for getting all the algebraically detailed analysis done in record time, and with perfect accuracy, leading to new tools and capabilities in nonlinear dynamics. Over the last twenty-five years we’ve developed software capable of taking sets of coupled nonlinear ordinary differential equations and solving them automatically, using adaptable perturbation methods, to arrive at analytical solutions for which the accuracy can be accurately controlled. In the last two years the spin-out company Symbolic Computational Dynamics Ltd has been created to explore commercial R&D for a generic nonlinear dynamics tool based on these techniques.
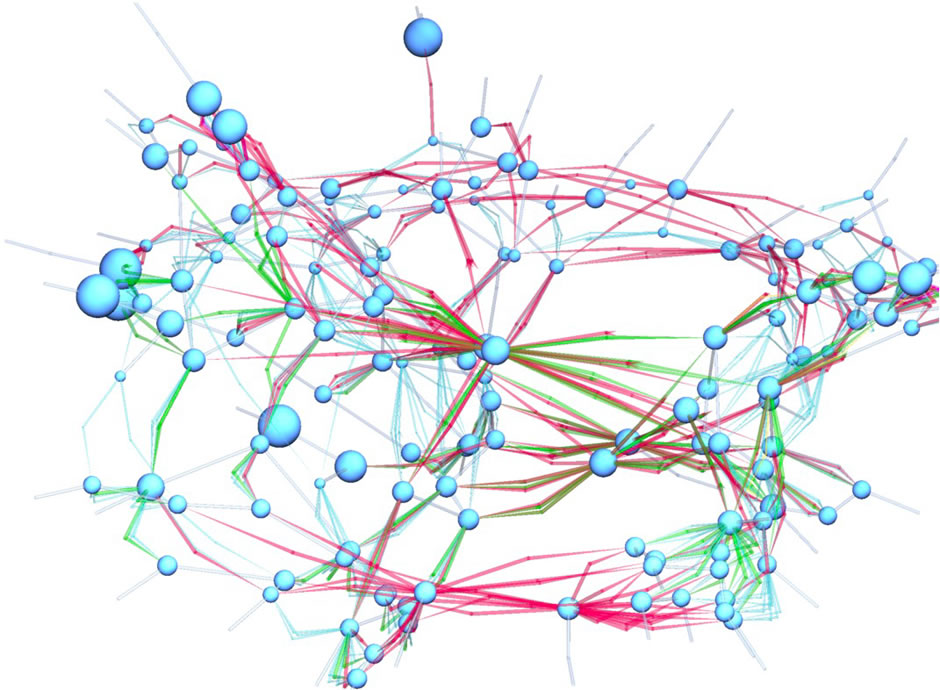
Figure 4 : Information structure from Symbolic Computational Dynamics analysis of aeroplane fuselage vibration study Copyright – Matthew P. Cartmell & Symbolic Computational Dynamics Ltd (2021)
In addition to nonlinear dynamics theory, software design, phenomenological studies in mechanical engineering, and using perturbation theories for applications in space systems, it’s become clear in the last few years that some of the thinking within nonlinear dynamics can be applied to the design of certain sorts of physical measurement systems required to make measurements in physics. Current research is taking a fresh look at the nineteenth century pendulum of Foucault, as a gyroscopic sensor for detecting the tiny physical motions that emerge directly from general relativity, and recently we’ve managed to show that in principle, such a measurement is conceptually possible on Earth, particularly as we move towards the poles. We continue to work towards a design for an experiment to do this more locally, bringing together nonlinear dynamics, general relativity and gravitoelectromagnetism in particular, astronomical data management, optical engineering, signal processing and statistical data analysis, and precision electro-mechanical engineering design.

Figure 5 : Upper connection point of Foucault test pendulum at the University of Strathclyde
Copyright – Matthew P. Cartmell